Self-supervised learning, which is widely popular in computer vision, focuses on extracting representations from unsupervised visual data. This article delves into the SWAV method, a robust self-supervised learning paper, from a mathematical perspective, providing insights and intuitions for why this method works. Additionally, it discusses the optimal transport problem with entropy constraint and its fast approximation, a key point of the SWAV method that may not be immediately evident from reading the paper.
For those interested in general aspects of self-supervised learning, such as augmentation, intuitions, softmax with temperature, and contrastive learning, a previous article is recommended for reference.
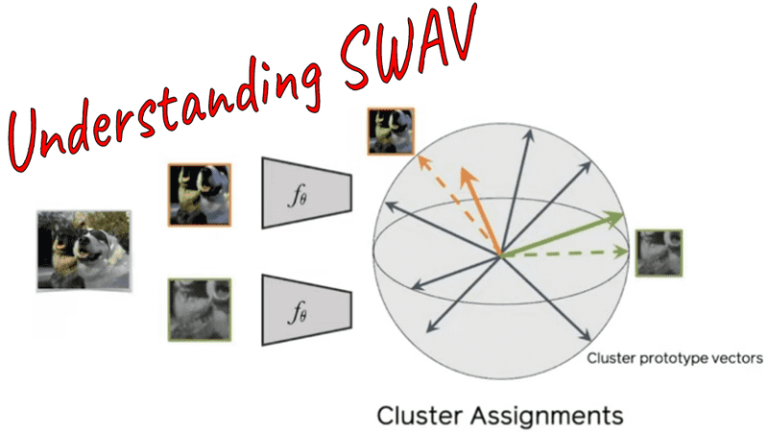
The SWAV method aims to compare image features using intermediate codes (soft classes) qt and qs. The method not only compares image features directly but also involves an intermediate step to create codes (targets) by assigning the image features to prototype vectors. This is different from contrastive learning methods, which directly compare image features from different transformations of the same images.
The SWAV method uses prototype vectors that are trainable vectors lying in the unit sphere, with their main purpose being to summarize the dataset and move based on over-represented features. By using L2-norm trick and applying L2-normalization to the features and prototypes throughout training, the method aims to achieve smooth change in assignments on the surface of the sphere.
The SWAV method involves multiple steps, including creating views from input images, calculating image feature representations, softmax-normalized similarities between all image features and prototypes, and calculating the code matrix Q iteratively.
In order to estimate the optimal code matrix Q, the method uses the Optimal Transport Problem with Entropic Constraint and makes use of the Sinkhorn-Knopp algorithm to efficiently approximate Q in each forward pass. The solution involves enforcing an entropy term to control the smoothness of the solution, allowing for a probabilistic interpretation while avoiding mode collapse.
The method’s experiments have shown that it converges faster and is less sensitive to batch size compared to other methods, making it a promising approach in self-supervised learning. Additionally, the multi-crop augmentation strategy was proposed to further improve representations. With four local views in addition to two global views, multi-crop has shown promising results in self-supervised learning.
In conclusion, the SWAV method offers a valuable contribution to self-supervised learning, providing a detailed mathematical analysis and practical insights into its effectiveness. Whether it’s the theoretical understanding or practical implementation, SWAV has the potential to make significant advancements in self-supervised learning in computer vision.