Traditionally, datasets in Deep Learning applications such as computer vision and NLP are typically represented in the euclidean space. Recently though there is an increasing number of non-euclidean data that are represented as graphs.
To this end, Graph Neural Networks (GNNs) are an effort to apply deep learning techniques in graphs. The term GNN is typically referred to a variety of different algorithms and not a single architecture. As we will see, a plethora of different architectures have been developed over the years. To give you an early preview, here is a diagram presenting the most important papers on the field. The diagram has been borrowed from a recent review paper on GNNs by Zhou J. et al.
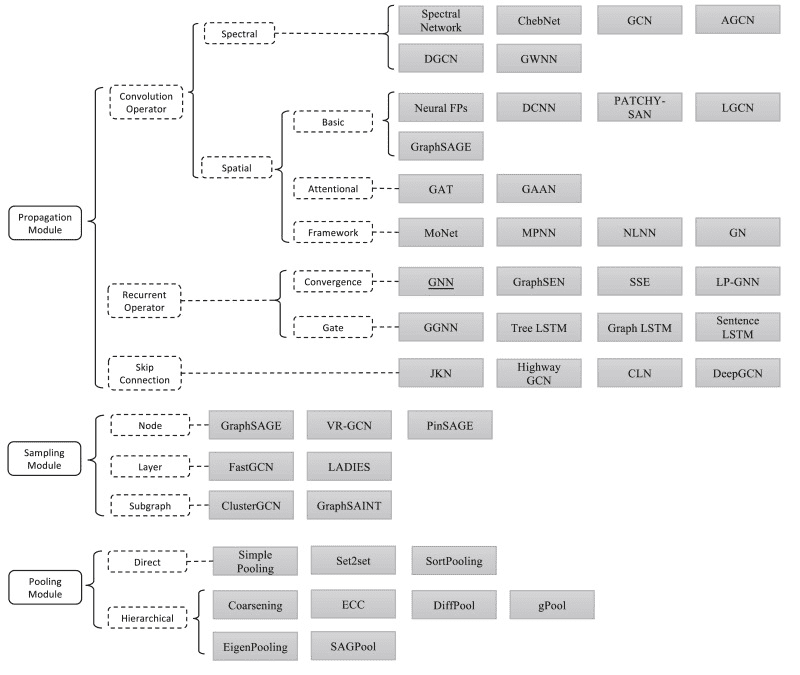
Source: Graph Neural Networks: A Review of Methods and Applications
Before we dive into the different types of architectures, let’s start with a few basic principles and some notation.
Graph basic principles and notation
Graphs consist of a set of nodes and a set of edges. Both nodes and edges can have a set of features. From now on, a node’s feature vector will be denoted as hih_ihi, where iii is the node’s index. Similarly an edge’s feature vector will be denoted as eije_{ij}eij, where iii, jjj are the nodes that the edge is attached to.
As you might also know, graphs can be directed, undirected, weighted and weighted. Thus each architecture may be applied only to a type of graph or to all of them.
So can we start developing a Graph Neural Network?
The basic idea behind most GNN architectures is graph convolution. In essence, we try to generalize the idea of convolution into graphs. Graphs can be seen as a generalization of images where every node corresponds to a pixel connected to 8 (or 4) adjacent neighbours. Since CNNs take advantage of convolution with such great success, why not adjust this idea into graphs?
Graph convolution
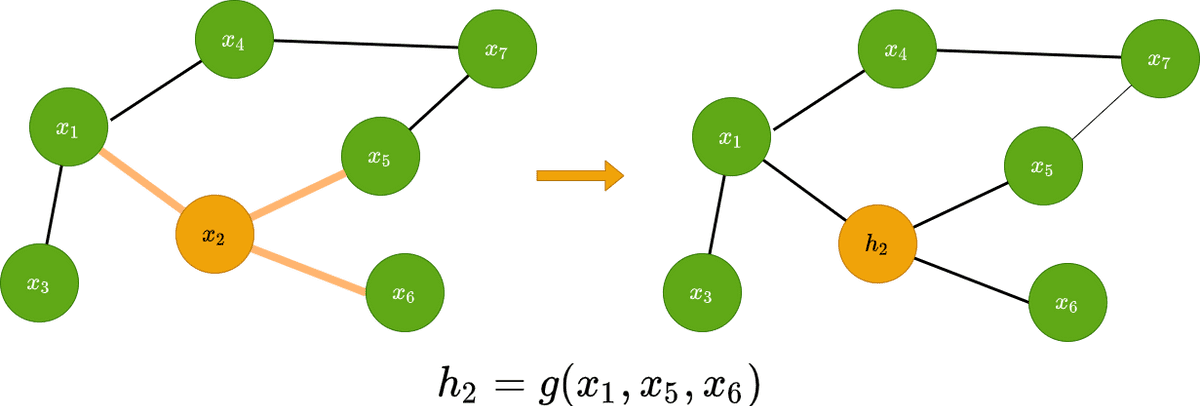
Graph convolution predicts the features of the node in the next layer as a function of the neighbours’ features. It transforms the node’s features xix_ixi in a latent space hih_ihi that can be used for a variety of reasons.
Visually this can be represented as follows:
But what can we actually do with these latent node features vectors? Typically all applications fall into one of the following categories:
Node classification
Edge classification
Graph classification
Node classification
If we apply a shared function fff to each of the latent vectors hih_ihi, we can make predictions for each of the nodes. That way we can classify nodes based on their features:
Here are the rest of the GNN architectures
…
…
…
…
…
…
and the rest of the text continues as it is.