This article is aimed at those who are curious about understanding the inner workings of self-attention. Instead of diving straight into complex transformer papers, it takes a step back to explore various perspectives on the attention mechanism.
After spending months studying this topic, I uncovered hidden insights that shed light on how content-based attention works.
The motivation for delving deeper into self-attention stems from the lack of clear explanations on why multi-head self-attention is effective. Renowned researchers like hadamaru from Google Brain have highlighted the importance of this mechanism post 2018.
In summary, there are two types of parallel computations embedded in self-attention, which we will dissect and analyze. The aim is to provide diverse perspectives on the effectiveness of multi-head self-attention.
If you’re interested in gaining a high-level understanding of attention and transformers, check out introductory articles or explore open-source libraries for implementations.
To bolster your PyTorch fundamentals, consider learning how to construct Deep Learning models using PyTorch. Use the code aisummer35 for an exclusive 35% discount on your favorite AI blog!
Self-attention as two matrix multiplications
The Math
In our discussion, we’ll focus on self dot-product attention without multiple heads for clarity. We begin with input matrix X and trainable weight matrices WQ, WK, and WV.
Here, X is of shape batch x tokens x dmodel, where:
- batch refers to the batch size
- tokens represent the number of elements in the sequence
- dmodel signifies the size of the embedding vector for each input element
Next, we create three distinct representations (query, key, value) by multiplying each with their respective weight matrices:
Q = XWQ, K = XWK, V = XWV, each of shape batch x tokens x dk.
The attention layer is defined as: Y = Attention(Q, K, V) = softmax(QKT/dk)V.
The dot product yields attention scores, indicating the level of similarity between elements. Higher scores imply greater attention weights, making it a measure of similarity.
An Intuitive Illustration
Consider a scenario where the queries, keys, and vectors come from different sequences. We illustrate this concept using a case with a query sequence of 4 tokens and an associative sequence with 5 tokens.
Both sequences have vectors of dimension dmodel=3 in our example. Self-attention can then be conceptualized as two matrix multiplications.
A visual representation can aid in better understanding:
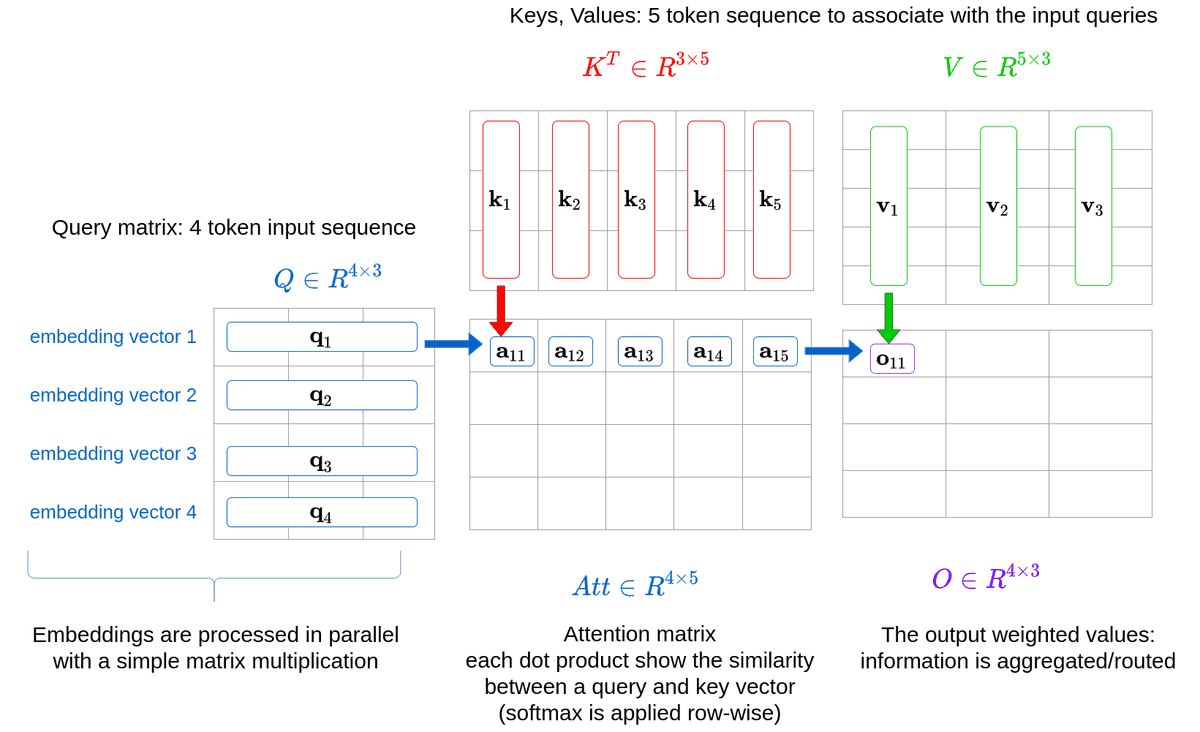
Collating all queries allows for matrix multiplication instead of computing each query separately. This parallelization through matrix multiplication is key to processing queries independently, enhancing efficiency.
The Query-Key Matrix Multiplication
The content-based attention architecture comprises distinct query, key, and value representations. Here, the query matrix serves as the “search,” while the keys guide where to look, and values provide the relevant content.
Key insights:
- Keys act as intermediaries between queries and values.
- Dot products between keys and queries determine the attention allocation.
- Keys dictate the attention weights based on specific queries.
Attention weights, calculated through softmax, influence the final weighted value. The weights from a query denote respective outputs.
The Attention V Matrix Multiplication
Weights (αij) derived from queries are employed to obtain the weighted value. This mimics directed attention from queries to respective values.
Understanding Cross-Attention in Transformers
The encoder-decoder attention, known as cross-attention, serves a pivotal role in the transformer architecture. Keys and values are derived from the final encoded input representations post multiple encoder blocks.
Deciphering Multi-Head Attention
By decomposing attention into multiple heads, transformers engage in parallel and independent computations. This mirrors varying “linear views” of a single sequence.
Original multi-head attention formulation:
MultiHead(Q, K, V) = Concat(head1, …, headh) WO, where each head i denotes individual computations.
Benefits of multi-head attention:
- Decomposes the initial embedding dimension to enhance computational efficiency.
- Enables independent head computations combined post attention.
The contributions of each head are typically consolidated and processed through a linear layer to align output dimensions with input embedding sizes.
Parallelizing Independent Computations in Self-Attention
Representations stem from the same inputs but exist in lower dimensions per individual head, akin to batch computations. This parallelization strategy simplifies computations efficiently.
Parallelization depends on GPU thread utilization, assigning threads for both batch and head processing. By module-wise segmentation, parallelization overhead is minimized, enhancing computational speed.
Insights and Observations in the Attention Mechanism
Self-Attention Symmetry
Self-attention is not instantaneously reciprocal. Queries and keys might appear symmetric, but the mechanism is asymmetric in practice.
Insight 0: Understanding self-attention as non-symmetric.
Mathematically, the design favors directed graphs due to distinct weights on keys and queries. A symmetric self-attention system would necessitate shared projection matrices for both queries and keys.
Incidentally, most papers opt for shared projection matrices for queries and keys. This aids in advancing multi-head attention comprehension.
Attention as Local Information Routing
Novel insights elucidate attention as a routing solution for local information streams. Each head retains substantial information from inputs, affirming its role as an assimilating mechanism.
Contrary to popular belief, multiple heads primarily serve collective purposes, emphasizing shared data focus and representations.
Classification and Pruning of Encoder Weights
Attention weights vary in prominence based on positional, syntactical, or content-anchored relationships. Selective pruning based on weight classification enhances model efficiency and performance.
Key categories include positional, syntactical, and content-focused heads. Pruning optimizes model weights, refining overall performance with minimal head retention.
Common Projections in Attention Heads
Notable research points to convergence in projection matrices across heads, hinting at shared attention focus areas. Independent attention heads meld in learning, ultimately aligning their focus within mutual subspace sectors.
Significance of Cross-Attention in Multi-Head Models
Experiments emphasize the intrinsic importance of cross-attention components in multi-head models. Pruning these components significantly impacts model performance, notably in encoder-decoder attention segments.
Low-Rank Implications in Post-Softmax Attention
Post-softmax computations in self-attention output low-rank results, enhancing computational efficiency. Singular value decomposition and rank analysis brought forth innovative linear attention models, redefining conventional attention frameworks.
Fast-Weight Memory Systems in Attention
Expanding on the fast-weight memory concept, attention manifests similar properties through weighted signal amplification. Insights explore the parallels between fast weights and query-key interactions in attention mechanisms.
Rank Collapse and Token Uniformity
Recent research recognizes a token uniformity bias and rank collapse vulnerability in self-attention systems. Mechanisms to counteract rank collapse through architectural adjustments are emerging, focusing on preserving model stability and complexity.
Layer Norm and Its Transfer Learning Impact
Amidst normalization complexities, layer norm emerges as a crucial linchpin fostering transfer learning adaptability in pretrained transformers. Selective fine-tuning of layer norm parameters introduces significant model refinements, notably in low-data settings.
Addressing Quadratic Complexity in Attention
Ongoing efforts seek to circumvent quadratic attention complexities through expertly crafted architectures. Sparsity-based methods like Big Bird and matrix rank approximations such as Linformer aim to overcome computational bottlenecks without compromising model performance.
In Conclusion
This in-depth exploration of the attention mechanism unearths myriad perspectives, shedding light on the nuanced workings of self-attention. The interplay of model components and insights gleaned from diverse studies enrich our understanding of content-based attention.
If you found this article enlightening, consider sharing it to spread knowledge among fellow enthusiasts. Your support is greatly appreciated!
Acknowledgment
A special mention to Yannic Kilcher for his insightful videos on transformers and attention mechanisms. His contributions have accelerated learning for researchers worldwide.
References
1. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., … & Polosukhin, I. (2017). Attention is all you need. arXiv preprint arXiv:1706.03762.
2. Michel, P., Levy, O., & Neubig, G. (2019). Are sixteen heads really better than one?. arXiv preprint arXiv:1905.10650.
3. Cordonnier, J. B., Loukas, A., & Jaggi, M. (2020). Multi-Head Attention: Collaborate Instead of Concatenate. arXiv preprint arXiv:2006.16362.
4. Voita, E., Talbot, D., Moiseev, F., Sennrich, R., & Titov, I. (2019). Analyzing multi-head self-attention: Specialized heads do the heavy lifting, the rest can be pruned. arXiv preprint arXiv:1905.09418.
5. Schlag, I., Irie, K., & Schmidhuber, J. (2021). Linear Transformers Are Secretly Fast Weight Memory Systems. arXiv preprint arXiv:2102.11174.
6. Yihe Dong et al. 2021. Attention is not all you need: pure attention loses rank doubly exponentially with depth
7. Wang, S., Li, B., Khabsa, M., Fang, H., & Ma, H. (2020). Linformer: Self-attention with linear complexity. arXiv preprint arXiv:2006.04768.
8. Tay, Y., Dehghani, M., Abnar, S., Shen, Y., Bahri, D., Pham, P., … & Metzler, D. (2020). Long Range Arena: A Benchmark for Efficient Transformers. arXiv preprint arXiv:2011.04006.
9. Zaheer, M., Guruganesh, G., Dubey, A., Ainslie, J., Alberti, C., Ontanon, S., … & Ahmed, A. (2020). Big bird: Transformers for longer sequences. arXiv preprint arXiv:2007.14062.
10. Lu, K., Grover, A., Abbeel, P., & Mordatch, I. (2021). Pretrained Transformers as Universal Computation Engines. arXiv preprint arXiv:2103.05247.
