I was very curious to see how JAX is compared to Pytorch or Tensorflow. I decided that the best way to compare frameworks is to build the same thing from scratch in both of them. In this article, I am developing a Variational Autoencoder with JAX, Tensorflow, and Pytorch simultaneously. I will provide the code for each component side by side in order to identify differences, similarities, weaknesses, and strengths.
Shall we begin?
Prologue
Before we explore the code, there are a few things to note:
I will use Flax on top of JAX, which is a neural network library developed by Google. It contains many ready-to-use deep learning modules, layers, functions, and operations.
For the Tensorflow implementation, I will rely on Keras abstractions.
For Pytorch, I will use the standard nn.module.
Since most of us are somewhat familiar with Tensorflow and Pytorch, I will focus more on JAX and Flax. Throughout the article, I will explain unfamiliar concepts to provide a light tutorial on Flax.
Additionally, I assume that you are acquainted with the basic principles behind VAEs. If not, you can refer to my previous article on latent variable models. If everything seems clear, let’s move forward.
Quick recap: The vanilla Autoencoder consists of an Encoder and a Decoder. The encoder converts the input to a latent representation zzz, and the decoder attempts to reconstruct the input based on that representation. In Variational Autoencoders, stochasticity is added to the mix, as the latent representation provides a probability distribution. This is achieved using the reparametrization trick.

Image by author
The encoder
For the encoder, a simple linear layer followed by a RELU activation is sufficient for a toy example. The output of the layer will consist of both the mean and standard deviation of the probability distribution.
The Flax API’s basic building block is the Module abstraction, which we will utilize to implement our encoder in JAX. The module is part of the linen subpackage. Similar to Pytorch’s nn.module, we again need to define our class arguments. In Pytorch, we are used to declaring them inside the __init__ function and implementing the forward pass inside the forward method. In Flax, things are a little different. Arguments are defined either as dataclass attributes or as method arguments. Usually, fixed properties are defined as dataclass arguments while dynamic properties are defined as method arguments. Instead of implementing a forward method, we implement __call__.
The Dataclass module was introduced in Python 3.7 as a utility tool for creating structured classes, especially for storing data. These classes hold specific properties and functions to deal with the data and its representation, reducing a lot of boilerplate code compared to regular classes.
To create a new module in Flax, we need to:
- Initialize a class that inherits flax.linen.nn.Module
- Define the static arguments as dataclass arguments
- Implement the forward pass inside the __call_ method
To link the arguments with the model and be able to define submodules directly within the module, we also need to annotate the __call__ method with @nn.compact.
Note that instead of using dataclass arguments and the @nn.compact annotation, we could have declared all arguments inside a setup method in the same way as we do in Pytorch’s or Tensorflow’s __init__.
import numpy as np
import jax
import jax.numpy as jnp
from jax import random
from flax import linen as nn
from flax import optim
class Encoder(nn.Module):
latents: int
@nn.compact
def __call__(self, x):
x = nn.Dense(500, name=’fc1′)(x)
x = nn.relu(x)
mean_x = nn.Dense(self.latents, name=’fc2_mean’)(x)
logvar_x = nn.Dense(self.latents, name=’fc2_logvar’)(x)
return mean_x, logvar_x
import tensorflow as tf
from tensorflow.keras import layers
class Encoder(layers.Layer):
def __init__(self,
latent_dim=20,
name=’encoder’,
**kwargs):
super(Encoder, self).__init__(name=name, **kwargs)
self.enc1 = layers.Dense(500, activation=’relu’)
self.mean_x = layers.Dense(latent_dim)
self.logvar_x = layers.Dense(latent_dim)
def call(self, inputs):
x = self.enc1(inputs)
z_mean = self.mean_x(x)
z_log_var = self.logvar_x(x)
return z_mean, z_log_var
import torch
import torch.nn.functional as F
class Encoder(torch.nn.Module):
def __init__(self, latent_dim=20):
super(Encoder, self).__init__()
self.enc1 = torch.nn.Linear(784, 500)
self.mean_x = torch.nn.Linear(500, latent_dim)
self.logvar_x = torch.nn.Linear(500, latent_dim)
def forward(self, inputs):
x = self.enc1(inputs)
x = F.relu(x)
z_mean = self.mean_x(x)
z_log_var = self.logvar_x(x)
return z_mean, z_log_var
A few more things to notice here before we proceed:
Flax’s nn.linen package contains most deep learning layers and operations such as Dense, relu, and many more.
The code in Flax, Tensorflow, and Pytorch is almost indistinguishable from each other.
The decoder
In a very similar fashion, we can develop the decoder in all 3 frameworks. The decoder will consist of two linear layers that receive the latent representation zzz and output the reconstructed input.
Again, the implementations are very similar.
class Decoder(nn.Module):
@nn.compact
def __call__(self, z):
z = nn.Dense(500, name=’fc1′)(z)
z = nn.relu(z)
z = nn.Dense(784, name=’fc2′)(z)
return z
class Decoder(layers.Layer):
def __init__(self,
name=’decoder’,
**kwargs):
super(Decoder, self).__init__(name=name, **kwargs)
self.dec1 = layers.Dense(500, activation=’relu’)
self.out = layers.Dense(784)
def call(self, z):
z = self.dec1(z)
return self.out(z)
class Decoder(torch.nn.Module):
def __init__(self, latent_dim=20):
super(Decoder, self).__init__()
self.dec1 = torch.nn.Linear(latent_dim, 500)
self.out = torch.nn.Linear(500, 784)
def forward(self, z):
z = self.dec1(z)
z = F.relu(z)
return self.out(z)
Variational Autoencoder
To combine the encoder and the decoder, let’s introduce another class, called VAE, that represents the entire architecture. In addition, we need to write some code for the reparameterization trick. Overall, the encoder’s latent variable is reparameterized and fed to the decoder, which produces the reconstructed input.
As a reminder, here is an intuitive image that explains the reparameterization trick:
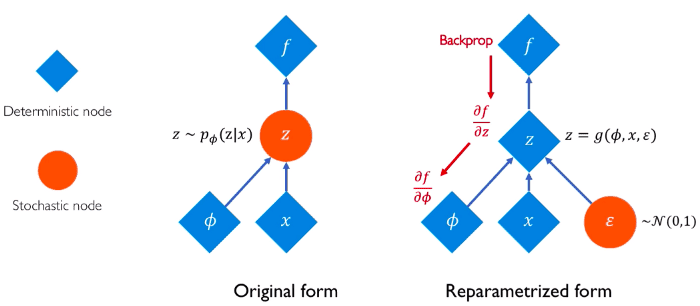
Source: Alexander Amini and Ava Soleimany, Deep Generative Modeling | MIT 6.S191, http://introtodeeplearning.com/
Notice that this time, in JAX we make use of the setup method instead of the nn.compact annotation. Also, see how similar the reparameterization functions are. Each framework uses its own functions and operations, but the general image is almost identical.
class VAE(nn.Module):
latents: int = 20
def setup(self):
self.encoder = Encoder(self.latents)
self.decoder = Decoder()
def __call__(self, x, z_rng):
mean, logvar = self.encoder(x)
z = reparameterize(z_rng, mean, logvar)
recon_x = self.decoder(z)
return recon_x, mean, logvar
def reparameterize(rng, mean, logvar):
std = jnp.exp(0.5 * logvar)
eps = random.normal(rng, logvar.shape)
return mean + eps * std
def model():
return VAE(latents=LATENTS)
class VAE(tf.keras.Model):
def __init__(self,
latent_dim=20,
name=’vae’,
**kwargs):
super(VAE, self).__init__(name=name, **kwargs)
self.encoder = Encoder(latent_dim=latent_dim)
self.decoder = Decoder()
def call(self, inputs):
z_mean, z_log_var = self.encoder(inputs)
z = self.reparameterize(z_mean, z_log_var)
reconstructed = self.decoder(z)
return reconstructed, z_mean, z_log_var
class VAE(torch.nn.Module):
def __init__(self, latent_dim=20):
super(VAE, self).__init__()
self.encoder = Encoder(latent_dim)
self.decoder = Decoder(latent_dim)
def forward(self, inputs):
z_mean, z_log_var = self.encoder(inputs)
z = self.reparameterize(z_mean, z_log_var)
reconstructed = self.decoder(z)
return reconstructed, z_mean, z_log_var
Loss and Training step
When we start implementing the training step and the loss function, things start to differ slightly. However, the differences are minimal.
To fully leverage JAX capabilities, we need to incorporate automatic vectorization and XLA compilation into our code. This can be easily achieved using the vmap and jit annotations.
Additionally, we need to enable automatic differentiation, which can be done with the grad_fn transformation.
We will use the flax.optim package for optimization algorithms.
Another small difference to note is how we pass data to our model. This can be accomplished through the apply method in the form of model().apply({‘params’: params}, batch, z_rng), where batch represents our training data.
@jax.vmap
def kl_divergence(mean, logvar):
return -0.5 * jnp.sum(1 + logvar – jnp.square(mean) – jnp.exp(logvar))
@jax.vmap
def binary_cross_entropy_with_logits(logits, labels):
logits = nn.log_sigmoid(logits)
return -jnp.sum(labels * logits + (1. – labels) * jnp.log(-jnp.expm1(logits)))
@jax.jit
def train_step(optimizer, batch, z_rng):
def loss_fn(params):
recon_x, mean, logvar = model().apply({‘params’: params}, batch, z_rng)
bce_loss = binary_cross_entropy_with_logits(recon_x, batch).mean()
kld_loss = kl_divergence(mean, logvar).mean()
loss = bce_loss + kld_loss
return loss, recon_x
grad_fn = jax.value_and_grad(loss_fn, has_aux=True)
_, grad = grad_fn(optimizer.target)
optimizer = optimizer.apply_gradient(grad)
return optimizer
def kl_divergence(mean, logvar):
return -0.5 * tf.reduce_sum(
1 + logvar – tf.square(mean) –
tf.exp(logvar), axis=1)
def binary_cross_entropy_with_logits(logits, labels):
logits = tf.math.log(logits)
return – tf.reduce_sum(
labels * logits +
(1-labels) * tf.math.log(- tf.math.expm1(logits)),
axis=1
)
@tf.function
def train_step(model, x, optimizer):
with tf.GradientTape() as tape:
recon_x, mean, logvar = model(x)
bce_loss = tf.reduce_mean(binary_cross_entropy_with_logits(recon_x, batch))
kld_loss = tf.reduce_mean(kl_divergence(mean, logvar))
loss = bce_loss + kld_loss
print(loss, kld_loss, bce_loss)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables)
def final_loss(reconstruction, train_x, mu, logvar):
BCE = torch.nn.BCEWithLogitsLoss(reduction=’sum’)(reconstruction, train_x)
KLD = -0.5 * torch.sum(1 + logvar – mu.pow(2) – logvar.exp())
return BCE + KLD
def train_step(train_x):
train_x = torch.from_numpy(train_x)
optimizer.zero_grad()
reconstruction, mu, logvar = model(train_x)
loss = final_loss(reconstruction, train_x, mu, logvar)
running_loss += loss.item()
loss.backward()
optimizer.step()
Remember that VAEs are trained by maximizing the evidence lower bound, known as ELBO.
Lθ,ϕ(x)=Eqϕ(z∣x)[logpθ(x∣z)]−KL(qϕ(z∣x)∣∣pθ(z))
* Disclosure: Please note that some of the links above might be affiliate links, and at no additional cost to you, we will earn a commission if you decide to make a purchase after clicking through.
Training loop
Finally, it’s time for the entire training loop which will execute the train_step function iteratively.
In Flax, the model needs to be initialized before training, which is done by calling the init function such as: params = model().init(key, init_data, rng)[‘params’]. A similar initialization is required for the optimizer as well: optimizer = optim.Adam( learning_rate = LEARNING_RATE ).create( params ).
Use jax.device_put to transfer the optimizer into the GPU’s memory.
rng = random.PRNGKey(0)
rng, key = random.split(rng)
init_data = jnp.ones((BATCH_SIZE, 784), jnp.float32)
params = model().init(key, init_data, rng)[‘params’]
optimizer = optim.Adam(learning_rate=LEARNING_RATE).create(params)
optimizer = jax.device_put(optimizer)
rng, z_key, eval_rng = random.split(rng, 3)
z = random.normal(z
