Recommendation systems are some of the most popular applications of machine learning on today’s websites and platforms. With the rise of eCommerce, personalized suggestions to clients are necessary for e-stores to distinguish themselves. Now, recommendation systems are at the core of online services such as Amazon, Netflix, Youtube, Spotify.
But what, exactly, is a recommendation system? Wikipedia defines it as “a subclass of information filtering system that seeks to predict the ‘rating’ or ‘preference’ a user would give to an item.”
TL;DR
This article will explore the most popular architectures for recommendation systems. It will start with primitive strategies like collaborative and content-based filtering and continue with state-of-the-art deep learning-based methods.
For a comprehensive approach to recommender systems, we highly recommend the Recommender Systems Specialization by the University of Michigan.
Problem Formulation
In most cases, we start with a number of items (products, videos, songs, etc.). Each item has a set of characteristics/features that define it. Our goal is to build a model that predicts items that a user may have an interest in. We typically have a form of score that evaluates the item’s relevancy and some sort of feedback that we get from users.
Now that we have a clear picture of the basics, let’s continue with the fundamental techniques.
Content-based filtering
Content-based filtering uses the similarity between items to recommend items similar to what a user likes.
Typically, each item with its features is mapped to a low-dimensional embedding space. Then, using a similarity measure, one can identify items in the same neighborhood on the embedding space and suggest those items to the users. The similarity function can be simple functions such as the dot-product, or the Euclidean distance, or more complex ones.
Mathematically, we have:
Given a query item q and a similarity measure s(q,x), the model will look for an item xxx that is close to q based on their similarity. For example:
- Given a query item q = [1,4,5] and a set of items (x1,x2,x3) = ([2,3,2],[1,0,0],[4,5,1]), the model will calculate the similarity of q with all items and selects the one with the smaller. The model will recommend the first item to the user.
Collaborative filtering
Collaborative filtering (CF) is a traditional approach that follows a simple principle: We should recommend items to a client based on the inputs or actions of other clients (preferably similar ones).
One approach is to look at similar users and recommend items that they like. This is called user-based CF. In the above table, we can see that users 1 and 3 have similar tastes in items (they both like item 1 and dislike item 3). So if we’d want to recommend an item to user 3, we would probably pick item 5 because user 1 seems to really like it. A different approach is to find similar items based on ratings given by other users. This is called item-based CF. Since user 1 likes item 1, we need to find an item that other users have rated similarly. We can see that the ratings between item 1 and item 3 are very close so item 3 is a natural choice to recommend to user 3. As we did in content-based systems, the similarity between users or items based on the ratings can be formulated using a similarity measure s(q,x). Both of the above approaches fall in the category of memory-based CF.
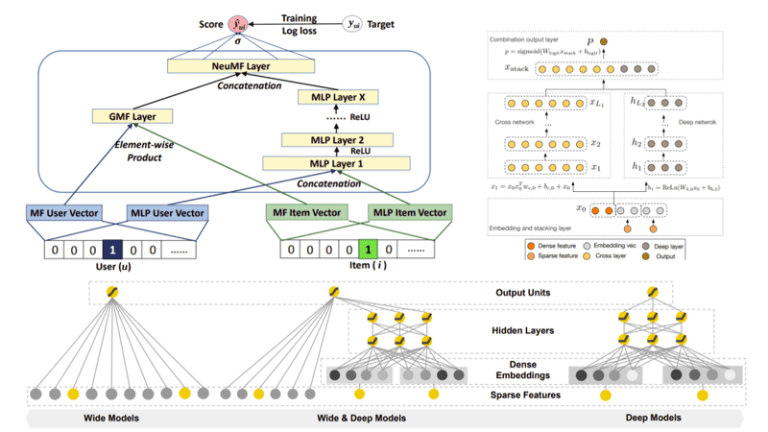
Model-based CF tries to model the interaction matrix between items and users. Each user and item can be mapped into an embedding space based on their features. The embeddings can be learned using a machine learning model so that close embeddings will correspond to similar items/users. This brings us to the most important model for recommendation systems: Matrix Factorization. In simple terms, Matrix Factorization (MF) algorithms work by decomposing the user-item interaction matrix into the product of two lower dimensionality rectangular matrices. Suppose that we denote the interaction matrix A, where m is the number of users and n the number of items. In practice, we also introduce a set of biases b_u and b_v for users and items, respectively. Many loss functions have been proposed over the years to train such models. The most simple one is the squared distance. Once we have trained an MF model, we have a way to predict the interaction between a user and a model. Recommendation with Autoencoders One very interesting idea is the utilization of Autoencoder in recommender systems.
Deep Learning-based Recommendation systems
Before we explore some state-of-the-art architectures, let’s discuss a few key ideas of deep learning-based methods. It’s undeniable that deep networks are excellent feature extractors and that’s why they are ideal for recommendation systems. Their ability to capture contextual information and generate user/item compact embeddings is unparalleled.
Deep Content-based recommendation
That’s why Deep Learning can be used for standard content-based recommendations. By using a neural network, we can construct high-quality low-dimensional embeddings and recommend items close in the embedding space. This idea can be extended into content embeddings (Content2Vec) where we can represent all kinds of items in an embedding space; whether the items are images, text, songs etc. Then we use a pair-wise item similarity metric to generate recommendations. Transfer learning can obviously play a major role in this approach. The content embeddings can be used either in a content-based strategy or as extra information on CF techniques, as we will see.
Candidate Generation and Ranking
One frequent idea on systems with a huge amount of items and users is to split the recommendation pipeline into two steps: candidate generation and ranking. Candidate generation: First we generate a larger set of relevant candidates based on our query using some approach. This step is called Retrieval in literature Ranking: After candidate generation, another model ranks the candidates producing a list of the top N recommendations. Re-Ranking: In some implementations, we perform another round of ranking based on additional criteria in order to remove some irrelevant candidates. As you may have imagined, the philosophy behind this is twofold. Now it’s time to continue with the most popular methods for building large-scale recommendation systems. In some categories we’ll look at specific architectures and in others we’ll discuss a more general approach.
Wide and Deep Learning
Wide and Deep Networks were originally proposed by Google and is an effort to combine traditional linear models with deep models. Shallow linear models are good at capturing and memorizing low-order interaction features, while deep networks are great at extracting high-level features How it works Wide and Deep models have proven to work very well for classification problems with sparse inputs such as recommender systems. Let’s take a closer look. Wide models are generalized linear models with non-linear transformations and they are trained on a wide set of cross-product transformations. The goal is to memorize specific useful feature combinations. On the other hand, deep models are learning items and user embeddings, which makes them able to generalize in unseen pairs without manual feature engineering. The fusion of wide and deep models combines the strengths of memorization and generalization and provides us with better recommendation systems. The two models are trained jointly with the same loss function.
An example of wide and deep learning: movie recommendations
Let’s assume that we want to recommend movies to users (e.g. we’re building a system for Netflix). Intuitively we can think that wide models will memorize things such as: “Bob liked Terminator 2” or “Alice hated The Avengers”. On the other hand, deep models will capture generic information such as: “Most teenage boys like action films” or “Middle-age women don’t like superhero movies”. The combination of these two helps us acquire better recommendations.
Deep Factorization Machines (DeepFm)
Deep Factorization Machines have gained a lot of popularity over the years. Before we analyze how they work, let’s first discuss simple Factorization Machines.
Factorization Machines (FM)
Factorization Machines is a generalized version of the linear regression model and the matrix factorization model. It improves upon them by supporting “n-way” variable interactions where n is the polynomial degree of the model. Usually, we use a degree of 2 but higher ones are also possible. Note though that in higher-degree FM, the numerical instability and the computational complexity increases. A cross-feature is a combination of 2 or more features which provides additional interaction information beyond individual features. The architecture 2-way FM is about a product of features, 3-way FM is about a product of pair-wise interactions, and so on. 2-way FM modeling the traditional continuous feature interactions, 3-way FM captures trilinear relationships between certain items 2-way FM: yi=f(wi,xi)=(wi1,kxi1+wi2,kxi2)bik(yi=1-k(∑i=1n∑j=i+1n〈vividj〉xi(1)xj(1)) (yi=f(wi,xi)=(wi1,kxi1+wi2,kxi2)bik(yi=1-k(∑i=1n∑j=i+1nvivj〈xi(1) xj(1))) The input to FM is the set of feature values x1⩵xn=(x1,x2,…,xn)x1⩵xn=(x1,x2,…,xn)x1⩵xn=(x1,x2,…,xn) of an input instance x, and the output is the predicted scalar prediction y=wf+∑j〈v,xdj〉y=wf+∑j〈v,xdj〉y=wf+∑j〈v,xdj〉. yyy represents the continuous target variable. w is a scalar, xi is a feature, v is a vector, and the number of total parameters in Factorization Machines is linear under the number of features and n is the factorization dimension. They become exponentially many when encoded into vector by OHE. Intuitively, the FM algorithm decomposes a complex feature combination into the product of much simpler 2-way interactions, and weights them linearly. y=wf+∑j〈v,xdj〉y=wf+∑j〈v,xdj〉y=wf+∑j〈v,xdj〉 The model will try to minimize the mean squared error between the predictions and the actual values. Again, we can see that it’s possible to include some regularizers here. FM will work with any classification feature, such as categorical variables, but also numerical data because it essentially maps feature vectors xv to real-valued weaker predictors wf+∑j〈v,xdj〉=xl+xn where l is the number of features. It usually does not create a model as large as Naive Bayes or Random Forests. Frequent sorting of m property values per factorization dimension tens, weeks, into roughly studies interactions of length much polynomial degrees with millions of features. Despite the benefits of their random ability to lightweight ones we usually use 2-way interactions. But they are limited with a power of two since the sum is easy to handle to <2-way FM: f(x)=wf+∑1≤i1 In simple terms, Matrix Factorization (MF) algorithms work by decomposing the user-item interaction matrix into the product of two lower dimensionality rectangular matrices. Suppose that we denote the interaction matrix A∈Rm×nA \in R^{m \times n} A∈Rm×n, where mmm is the number of users and nnn the number of items. We also denote U∈Rm×dU \in R^{m \times d}U∈Rm×d the user embedding matrix and V∈Rn×dV \in R^{n \times d} V∈Rn×d the item embedding matrix. Item and user embedding matrices UUU and VVV contain a compact representation of all items/users features respectively. The iiithrow in UUU gives us the embedding for the user iii, while the jjj row in VVV gives us the embedding for item jjj. The model tries to learn the matrices UUU and VVV so that UV=AAUV^T=AUVT=A. For example: Each element on the A matrix corresponds to the interaction of a specific user with a specific item. In practice, we also introduce a set of biases bub_ubu and bvb_vbv for users and items, respectively. Many loss functions have been proposed over the years to train such models: the most simple one is the squared distance from the observed values. Once we have trained an MF model, we have a way to predict the interaction between a user and a model. There is also a way to recommend a new item to a user, we simply get all the “ratings” and return the highest one. Nonetheless you have to consider the scaling of such methods for a huge number of items or users. And that brings us to… Before we explore some state-of-the-art architectures, let’s discuss a few key ideas of deep learning-based methods. It’s undeniable that deep networks are excellent feature extractors and that’s why they are ideal for recommendation systems. Their ability to capture contextual information and generate user/item compact embeddings is unparalleled. That’s why Deep Learning can be used for standard content-based recommendations. By using a neural network, we can construct high-quality low-dimensional embeddings and recommend items close in the embedding space. This idea can be extended into content embeddings (Content2Vec) where we can represent all kinds of items in an embedding space; whether the items are images, text, songs etc. Then we use a pair-wise item similarity metric to generate recommendations. Transfer learning can obviously play a major role in this approach. The content embeddings can be used either in a content-based strategy or as extra information on CF techniques, as we will see. One frequent idea on systems with a huge amount of items and users is to split the recommendation pipeline into two steps: candidate generation and ranking. Candidate generation: First we generate a larger set of relevant candidates based on our query using some approach. This step is called Retrieval in literature Ranking: After candidate generation, another model ranks the candidates producing a list of the top N recommendations Re-Ranking: In some implementations, we perform another round of ranking based on additional criteria in order to remove some irrelevant candidates. As you may have imagined, the philosophy behind this is twofold. While we have discussed the most popular methods for building large-scale recommendation systems, it’s important to understand the general approach. Let’s begin. Wide and Deep Networks were originally proposed by Google and is an effort to combine traditional linear models with deep models. Shallow linear models are good at capturing and memorizing low-order interaction features, while deep networks are great at extracting high-level features. The fusion of wide and deep models combines the strengths of memorization and generalization and provides us with better recommendation systems. The two models are trained jointly with the same loss function.Matrix Factorization

Source: developers.google.comDeep Learning-based Recommendation systems
Deep Content-based recommendation
Candidate Generation and Ranking
Wide and Deep Learning